一体化构建方法

提示

以力密度为未知数的节点力平衡方程

建立结构模型，对结构节点、单元进行标号，构建张力结构关联矩阵 $C_{s}$ :

\begin{matrix} (1) & C_{s} = [\begin{matrix} C & C_{f} \end{matrix}] \end{matrix}

其中： $C (\in R^{b \times n})$ 、 $C_{f} (\in R^{b \times n_{f}})$ 分别为自由节点关联矩阵、固定节点关联矩阵， $b$ 、 $n$ 、 $n_{f}$ 分别为单元、自由节点、固定节点数量。假定单元 $k$ 的两端点分别为节点 $i$ 、节点 $j$ ，则矩阵 $C_{s}$ 的 $k$ 行 $p$ 列为：

\begin{matrix} (2) & c_{s} (k, p) = {\begin{cases} 1 & , p = i \\ - 1 & , p = j \\ 0 & , p \neq i, j \end{cases} \end{matrix}

对每个自由节点，以单元力密度向量 $\vec{q}$ 为未知数，列力平衡方程：

\begin{matrix} (3) & {\begin{cases} C^{T} d i a g (C_{s} \vec{x_{s}}) \vec{q} & = - \vec{p_{x}} \\ C^{T} d i a g (C_{s} \vec{y_{s}}) \vec{q} & = - \vec{p_{y}} \\ C^{T} d i a g (C_{s} \vec{z_{s}}) \vec{q} & = - \vec{p_{z}} \end{cases} \end{matrix}

其中： $\vec{x_{s}} = {[\begin{matrix} x & \vec{x_{f}} \end{matrix}]}^{T}$ 、 $\vec{y_{s}} = {[\begin{matrix} y & \vec{y_{f}} \end{matrix}]}^{T}$ 、 $\vec{z_{s}} = {[\begin{matrix} z & \vec{z_{f}} \end{matrix}]}^{T}$ ， $\vec{x}$ 、 $\vec{y}$ 、 $\vec{z} (\in R^{n})$ 分别为自由节点 $x$ 、 $y$ 、 $z$ 坐标列向量：

\begin{matrix} (4) & {\begin{cases} \vec{x} & = (x_{1}, x_{2}, \dots, x_{n})^{T} \\ \vec{y} & = (y_{1}, y_{2}, \dots, y_{n})^{T} \\ \vec{z} & = (z_{1}, z_{2}, \dots, z_{n})^{T} \end{cases} \end{matrix}

$\vec{x_{f}}$ 、 $\vec{y_{f}}$ 、 $\vec{z_{f}} (\in R^{n_{f}})$ 分别为固定节点 $x$ 、 $y$ 、 $z$ 坐标列向量：

\begin{matrix} (5) & {\begin{cases} {\vec{x}}_{f} & = (x_{n + 1}, x_{n + 2}, \dots, x_{n + n_{f}})^{T} \\ {\vec{y}}_{f} & = (y_{n + 1}, y_{n + 2}, \dots, y_{n + n_{f}})^{T} \\ {\vec{z}}_{f} & = (z_{n + 1}, z_{n + 2}, \dots, z_{n + n_{f}})^{T} \end{cases} \end{matrix}

$\vec{p_{x}}$ 、 $\vec{p_{y}}$ 、 $\vec{p_{z}} (\in R^{n})$ 分别为自由节点 $x$ 、 $y$ 、 $z$ 方向外荷载：

\begin{matrix} (6) & {\begin{cases} {\vec{p}}_{x} & = (p_{x, 1}, x_{x, 2}, \dots, x_{x, n})^{T} \\ {\vec{p}}_{y} & = (p_{y, 1}, x_{y, 2}, \dots, x_{y, n})^{T} \\ {\vec{p}}_{z} & = (p_{z, 1}, x_{z, 2}, \dots, x_{z, n})^{T} \end{cases} \end{matrix}

$\vec{q} (\in R^{b}) = (q_{1}, \dots, q_{k}, \dots, q_{b})^{T}$ ，称为单元力密度列向量，元素 $q_{k}$ 为单元 $k$ 的预应力 $N_{k}$ 与长度 $l_{k}$ 的比值， $d i a g (\dots)$ 表示以 $(\dots)$ 为对角元素的方阵。

方程(3)进一步写为矩阵形式：

\begin{matrix} (7) & A \vec{q} = \vec{p} \end{matrix}

其中：

\begin{matrix} (8) & A (\in R^{3 n \times b}) = [\begin{matrix} C^{T} d i a g (C_{s} {\vec{x}}_{s}) \\ C^{T} d i a g (C_{s} {\vec{y}}_{s}) \\ C^{T} d i a g (C_{s} {\vec{y}}_{s}) \end{matrix}] \end{matrix}

称为平衡矩阵， $\vec{p} (\in R^{3 n}) = - [\begin{matrix} {\vec{p}}_{x} \\ {\vec{p}}_{y} \\ {\vec{p}}_{z} \end{matrix}]$ ，称为节点外荷载列向量。

提示

现阶段sonew不考虑外荷载

单元预应力功能目标

单元预应力功能目标可表示为单元间力密度的相互关系：

\begin{matrix} (9) & [\begin{matrix} α_{1}, α_{2}, \dots, α_{b} \end{matrix}] \vec{q} = 0 \end{matrix}

如单元 $u$ 、 $v$ 的力密度比值等于 $α$ 可表示为： $q_{u} / q_{v} = α$ ，写为矩阵形式为：

\begin{matrix} (10) & [\begin{matrix} 0, \dots, 1, \dots, - α, \dots, 0 \end{matrix}] \vec{q} = 0 \end{matrix}

其预应力比值等于 $α$ 可表示为： $q_{u} / q_{v} = α l_{v} / l_{u}$ ，写为矩阵形式为：

\begin{matrix} (11) & [\begin{matrix} 0, \dots, 1, \dots, - α l_{v} / l_{u}, \dots, 0 \end{matrix}] \vec{q} = 0 \end{matrix}

预应力功能目标写成矩阵形式：

\begin{matrix} (12) & Ω \vec{q} = \vec{ω} \end{matrix}

其中： $Ω (\in R^{e \times b})$ 为单元预应力功能目标系数矩阵， $e$ 为单元预应力功能目标个数。

结构整体预应力水平

实际工程应用中，需要控制结构整体预应力水平，这里取单元力密度平方和为一常数，即：

\begin{matrix} (13) & \sum_{k = 1}^{b} q_{k}^{2} = q_{c}^{2} \end{matrix}

写为矩阵形式为：

\begin{matrix} (14) & {\vec{q}}^{T} \vec{q} = q_{c}^{2} \end{matrix}

其中： $q_{c}^{2}$ 为预应力总体水平系数。

提示

现阶段sonew只引入了此项预应力水平，且 $q_{c} = 1$ 。这将在提交计算时，由程序自动施加。

以节点坐标为未知数的节点力平衡方程

对每个自由节点，以节点坐标 $\vec{x}$ 、 $\vec{y}$ 、 $\vec{z}$ 为未知数，列力平衡方程：

\begin{matrix} (15) & {\begin{cases} C^{T} d i a g (\vec{q}) C \vec{x} + C^{T} d i a g (\vec{q}) C_{f} {\vec{x}}_{f} & = - \vec{p_{x}} \\ C^{T} d i a g (\vec{q}) C \vec{y} + C^{T} d i a g (\vec{q}) C_{f} {\vec{y}}_{f} & = - \vec{p_{y}} \\ C^{T} d i a g (\vec{q}) C \vec{z} + C^{T} d i a g (\vec{q}) C_{f} {\vec{z}}_{f} & = - \vec{p_{z}} \end{cases} \end{matrix}

写成矩阵形式：

\begin{matrix} (16) & [\begin{matrix} D & 0 & 0 \\ 0 & D & 0 \\ 0 & 0 & D \end{matrix}] [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \end{matrix}] = [\begin{matrix} - {\vec{p}}_{x} - D_{f} {\vec{x}}_{f} \\ - {\vec{p}}_{y} - D_{f} {\vec{y}}_{f} \\ - {\vec{p}}_{z} - D_{f} {\vec{z}}_{f} \end{matrix}] \end{matrix}

其中： $D (\in R^{n \times n}) = C^{T} d i a g (\vec{q}) C$ ， $D_{f} (\in R^{n \times n_{f}}) = C^{T} d i a g (\vec{q}) C_{f}$ ，式(15)可进一步简化为：

\begin{matrix} (17) & D_{g} [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \end{matrix}] = [\begin{matrix} {\vec{p}}_{x f} \\ {\vec{p}}_{y f} \\ {\vec{p}}_{x f} \end{matrix}] \end{matrix}

其中：

\begin{matrix} (18) & D_{g} (\in R^{3 n \times 3 n}) = [\begin{matrix} D & 0 & 0 \\ 0 & D & 0 \\ 0 & 0 & D \end{matrix}] \end{matrix}

称为力密度矩阵， ${\vec{P}}_{x f}$ 、 ${\vec{P}}_{y f}$ 、 ${\vec{P}}_{z f}$ 为考虑支座反力的节点外荷载向量。

节点坐标功能目标

节点坐标功能目标可表示为节点坐标的相互关系，其第 $k$ 个约束关系可表示为：

\begin{matrix} (19) & [\begin{matrix} ψ_{k, 1}, ψ_{k, 2}, \dots, ψ_{k, 3 n} \end{matrix}] [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \end{matrix}] = ψ_{k} \end{matrix}

如 $i$ 节点 $x$ 方向坐标固定于 $x_{i}^{'}$ 可表示为：

\begin{matrix} (20) & [\begin{matrix} 0, \dots, 1, \dots, 0 \end{matrix}] \vec{x} = x_{i}^{'} \end{matrix}

如 $i$ 、 $j$ 节点 $x$ 方向坐标相同可表示为：

\begin{matrix} (21) & [\begin{matrix} 0, \dots, 1, \dots, - 1, \dots, 0 \end{matrix}] \vec{x} = 0 \end{matrix}

节点坐标功能目标写成矩阵形式：

\begin{matrix} (22) & Ψ [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \end{matrix}] = \vec{ψ} \end{matrix}

其中： $Ψ (\in R^{m \times 3 n})$ 为节点坐标功能目标系数矩阵， $m$ 为节点坐标功能目标个数， $\vec{ω}$ 为节点坐标功能目标相关系数。

基本方程组集

将式(7)、(12)、(14)、(16)、(22)组集，并注意到： $d i a g (\vec{q}) C_{f} {\vec{x}}_{f} = d i a g (C_{f} {\vec{x}}_{f}) \vec{q}$ ，可得下式：

\begin{matrix} (23) & [\begin{matrix} C^{T} d i a g (\vec{q}) C & 0 & 0 & C^{T} d i a g (C_{f} {\vec{x}}_{f}) \\ 0 & C^{T} d i a g (\vec{q}) C & 0 & C^{T} d i a g (C_{f} {\vec{y}}_{f}) \\ 0 & 0 & C^{T} d i a g (\vec{q}) C & C^{T} d i a g (C_{f} {\vec{z}}_{f}) \\ 0 & 0 & 0 & C^{T} d i a g (C_{s} {\vec{x}}_{s}) \\ 0 & 0 & 0 & C^{T} d i a g (C_{s} {\vec{y}}_{s}) \\ 0 & 0 & 0 & C^{T} d i a g (C_{s} {\vec{z}}_{s}) \\ Ψ & 0 \\ 0 & 0 & 0 & Ω \\ 0 & 0 & 0 & {\vec{q}}^{T} \end{matrix}] [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \\ \vec{q} \end{matrix}] = [\begin{matrix} - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ \vec{ψ} \\ \vec{ω} \\ {\vec{q}}_{c}^{2} \end{matrix}] \end{matrix}

或：

\begin{matrix} (24) & [\begin{matrix} D & 0 & 0 & D_{f x} \\ 0 & D & 0 & D_{f y} \\ 0 & 0 & D & D_{f z} \\ 0 & 0 & 0 & A_{x} \\ 0 & 0 & 0 & A_{y} \\ 0 & 0 & 0 & A_{z} \\ Ψ & 0 \\ 0 & 0 & 0 & Ω \\ 0 & 0 & 0 & {\vec{q}}^{T} \end{matrix}] [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \\ \vec{q} \end{matrix}] = [\begin{matrix} - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ \vec{ψ} \\ \vec{ω} \\ {\vec{q}}_{c}^{2} \end{matrix}] \end{matrix}

其中：

\begin{matrix} (25) & D (\in R^{n \times n}) = C^{T} d i a g (\vec{q}) C \end{matrix}

\begin{matrix} (26) & {\begin{cases} D_{f x} (\in R^{n \times b}) = C^{T} d i a g (C_{f} {\vec{x}}_{f}) \\ D_{f y} (\in R^{n \times b}) = C^{T} d i a g (C_{f} {\vec{y}}_{f}) \\ D_{f z} (\in R^{n \times b}) = C^{T} d i a g (C_{f} {\vec{z}}_{f}) \end{cases} \end{matrix}

$Ψ \in R^{m \times 3 n}$ ， $Ω \in R^{e \times b}$ 。

进一步简化得到找形找力一体化方程：

\begin{matrix} (27) & Λ \vec{ζ} = \vec{γ} \end{matrix}

其中：

\begin{matrix} (28) & Λ (\in R^{(6 n + m + e + 1) \times (3 n + b)}) = [\begin{matrix} D & 0 & 0 & D_{f x} \\ 0 & D & 0 & D_{f y} \\ 0 & 0 & D & D_{f z} \\ 0 & 0 & 0 & A_{x} \\ 0 & 0 & 0 & A_{y} \\ 0 & 0 & 0 & A_{z} \\ Ψ & 0 \\ 0 & 0 & 0 & Ω \\ 0 & 0 & 0 & {\vec{q}}^{T} \end{matrix}] \end{matrix}

\begin{matrix} (29) & \vec{ζ} (\in R^{3 n + b}) = [\begin{matrix} \vec{x} \\ \vec{y} \\ \vec{z} \\ \vec{q} \end{matrix}] \end{matrix}

\begin{matrix} (30) & \vec{γ} (\in R^{6 n + m + e + 1}) = [\begin{matrix} - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ - {\vec{p}}_{x} \\ - {\vec{p}}_{y} \\ - {\vec{p}}_{z} \\ \vec{ψ} \\ \vec{ω} \\ {\vec{q}}_{c}^{2} \end{matrix}] \end{matrix}

$Λ$ 、 $\vec{ζ}$ 、 $\vec{γ}$ 分别为找形找力一体化矩阵、坐标、系数。

方程(27)将节点坐标、单元力密度两类完全不同的物理量统一到单一方程组，不再区分“形”与“力”，并综合节点坐标功能目标、单元预应力功能目标及结构整体预应力水平，形成形态构建一体化方程。

方程的直接求解

方程(27)系数矩阵相对结构有限元刚度矩阵有以下特点：

行数大于列数。
为非对称矩阵。
一般情况下非正定。
含有未知数，方程(27)高度非线性。

由于初始结构并非在每个自由节点处均满足力平衡方程，方程(27)增广矩阵的秩大于系数矩阵的秩，即 $r a n k ([\begin{matrix} Λ \vec{γ} \end{matrix}]) > r a n k (Λ)$ ，方程(27)无解，只能求其近似解。常规做法采用最小二乘法进行迭代求解，其近似解为：

\begin{matrix} (31) & {\vec{ζ}}_{(k + 1)} = Λ_{(k)}^{+} \vec{γ} \end{matrix}

其中： $Λ^{+} (\in R^{(3 n + b) \times (6 n + m + e + 1)})$ 为矩阵 $Λ$ 的广义逆，即

\begin{matrix} (32) & Λ^{+} = (Λ^{T} Λ)^{- 1} Λ^{T} \end{matrix}

直接求解存在两个问题：

方法对初始值非常敏感，迭代极易发散。
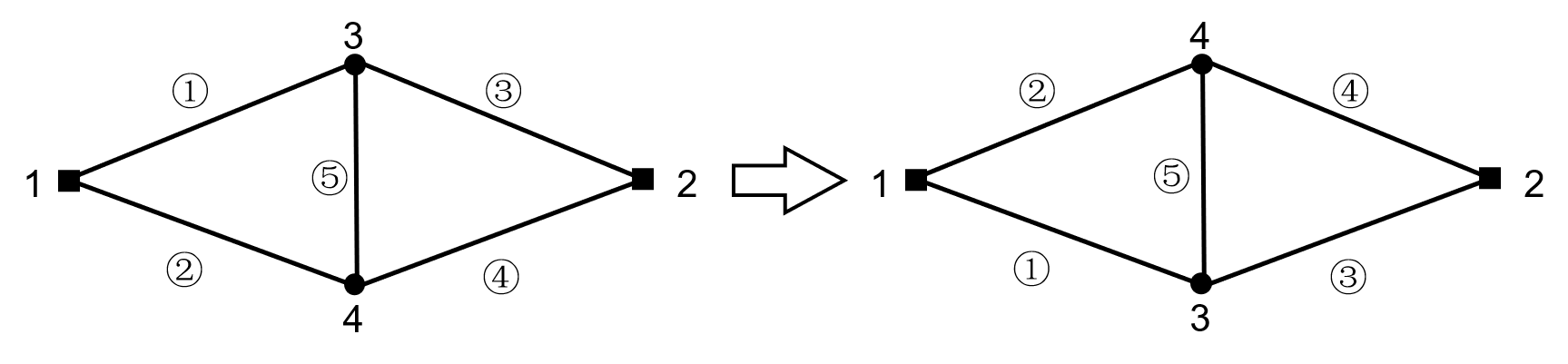
一些结构构建结果本身是多值的。例如平面索桁架，上下弦发生翻转后同样满足方程(27)。这使得迭代要么极易发散，要么收敛到错误结果。

平面索桁架上下弦翻转

方程的凸优化求解

为避免上述情况发生，必须改变求解策略。sonew将直接求解方程组问题转化为求解方程组误差最小的凸优化问题。同时附加不等式功能目标，进一步提高求解健壮性，并可避免多值问题。

提示

不等式约束将构建一道"铜墙铁壁"，迭代值很难突破此界限。
通过不等式约束，将不需要的多值屏蔽，使可行集为凸集。可行集为凸集的凸函数，是一定有唯一极小值的。
简单模型、简单功能目标可不设置不等式约束。

以下简述凸优化方法。

对于非线性方程组：

\begin{matrix} (33) & A x = b \end{matrix}

设：

\begin{matrix} (34) & \begin{matrix} f (x) = A x - b \\ F = 0.5 f^{T} f = 0.5 (A x - b)^{T} (A x - b) \end{matrix} \end{matrix}

求解方程(33)可看作求函数 $F$ 的极小值。当方程(33)有唯一解， $F$ 有唯一极小值，且极小值为0。

为实现不等式约束：

\begin{matrix} (35) & C x > d \end{matrix}

提示

小于类型的不等式，可通过两边取负，转化为大于类型不等式。

采用内点罚函数法，引入罚函数：

\begin{matrix} (36) & p_{i} = \frac{1}{C_{i} x - d_{i}} \end{matrix}

附带不等式约束的优化目标函数为：

\begin{matrix} (37) & Q = F + α P \end{matrix}

其中：

\begin{matrix} (38) & \begin{matrix} P = 0.5 p^{T} p \\ p = {[\begin{matrix} p_{1} & \dots & p_{i} & \dots & p_{n} \end{matrix}]}^{T} \end{matrix} \end{matrix}

迭代产生最小值 $Q (α)$ 及对应的 $x (α)$ ，不断缩小 $α$ 的值至零，即得到原问题的极小值 $F$ 及对应的 $x$ 。

一体化构建方法 ​

以力密度为未知数的节点力平衡方程 ​

单元预应力功能目标 ​

结构整体预应力水平 ​

以节点坐标为未知数的节点力平衡方程 ​

节点坐标功能目标 ​

基本方程组集 ​

方程的直接求解 ​

方程的凸优化求解 ​